티스토리 뷰
SAT 는 무엇인가?
SAT(Separating Axis Theorem)는 두 개의 볼록 다각형 또는 볼록 다면체가 충돌하지 않는지를 확인하는 데 사용되는 알고리즘이다.
- SAT(Separating Axis Theorem)
- 두 개의 볼록 다각형 또는 볼록 다면체가 충돌하지 않는지 확인하는 로직이다.
- SAT는 유명한 강체 충돌 탐색 알고리즘 중 하나이다.
- SAT는 오직 볼록 다면체(convex polygons)에서만 작용한다.
SAT에서 "충돌했다" 의 정의

위 이미지의 내용을 풀이하자면, 두 개의 도형을 분리할 수 있는 적어도 하나의 축이 주어진다면 SAT 관점에서 두 도형은
"충돌하지 않았다." 상태로 정의할 수 있다.
즉 두 도형을 분리할 수 있는 축이 하나도 존재하지 않을 때, 비로소 "충돌 했다" 으로 정의할 수 있겠다.
볼록 다면체(convex polygon)이는 무엇일까?
볼록 다면체는 모든 내부의 각이 180 미만인 도형을 말한다. 쉽게 말해서 다면체의 모든 면이 바깥쪽으로
볼록하게 튀어나온 도형을 말한다.

위 이미지를 보면 왼쪽 도형이 볼록 다면체이고 오른쪽이 오목 다면체이다.
이들의 차이점을 표로 비교해보면 다음과 같다.
| 구분 | convex polygon | concave polygon |
| 도형 내부에 두점을 잇는 선을 그렸을 때 | - 모든 선분이 도형 내부에 존재한다. | - 적어도 하나의 선이 도형 외부를 벗어난다. |
| 도형 내부의 각도 | - 모든 내각이 180 도 미만이다. | - 적어도 하나의 내각이 180 도 이상이다. |
| 예시 도형 | - 삼각형, 사각형, 육각형, 등.. | - 번개 모양, 화살촉모양, 등.. |
SAT의 축(Axis) 구하기
Axis 구하기 전에 고려해야 할 것
- 2D 평면 좌표 상에서 axis를 그리려고 하면 무한가지의 axis가 나오는데 이를 전부 연산해야 하나?
- Axis의 값은 평면 위의 좌표(x,y) 으로 생각하면 안된다.
Axis 정의하기
SAT에서 Axis는 두 개의 Convex polygon의 모서리의 법선벡터이다.
그런데 앞 절에서 말했던 SAT에서 충돌되지 않는 조건을 생각해보면 이런 궁금증이 생긴다.
"굳이 모서리의 법선 벡터여야 할 이유가 있을까? 다른 벡터로도 충분히 충돌을 검사할 수있지 않나?"
물론 굳이 법선벡터가 아니라도 다른 Axis를 이용하여 충분히 충돌을 비교할 수 있다.
그래도 아래의 이유로 인해서 SAT 알고리즘에서 두 도형 모서리의 법선벡터를 사용할 수 밖에 없어진다.
- 충돌 연산의 효율성: 두 도형 사이의 충돌여부를 판단한다고 무한가지의 Axis를 사용하는 것은 연산비용이 비싸다.
- 정확성: SAT는 모서리 사이 충돌을 검사하는 로직이므로 해당되는 모서리의 법선벡터만 있어도 매우 정확하다.

Axis 와 각 도형의 정점의 투영
먼저 Axis는 기울기만 가지고 있고 길이는 무한이라는 점을 알고 있어야 한다.
그러므로 우리는 Axis를 임의의 위치 위치시켜도 상관없어진다.

이동된 Axis에 각 도형의 정점들을 투영시키면 다음과 같이 된다.
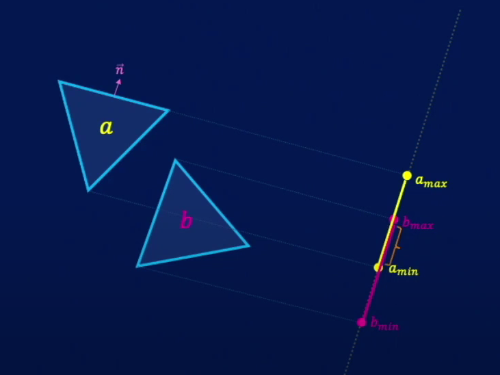
위 이미지에서 투영된 정점이 2개밖에 없는 이유는 다면체의 n개의 투영 정점 중 최대값과 최솟값만 정의 된다면
나머지 값들은 다 최대,최솟값의 법위 안에 위치하기 때문이다.
위 이미지에서는 a 도형과 b 도형을 하나의 Axis에 투영 시켰을 때 겹치는 구간이 발생하는 것을 알 수 있다.

이렇게 다른 축도 위의 과정과 똑같이 반복하다 보면 겹치지 않는 구간이 발생할 수 있다.
결국 위 이미지의 두 도형은 서로 충돌하고 있지 않은 상태로 결정 된다.
그럼 반대로 생각해서 두 도형의 법선 벡터 갯수만큼 반복하여 겹침검사를 했는데 축의 모든 케이스 가 겹쳐진다면
이는 두 도형이 서로 충돌하고 있는 상태로 결정된다.
MTV(Minimum Translation Vector) 연산 및 도형 이동
두 도형사이의 관계가 서로 겹쳐진 관계라면 이제 겹쳐진 길이만큼 도형을 이동시켜야 한다.
도형을 이동시키기 위해 MTV를 구해서 이를 도형 이동에 적용해야 한다.
여기서 MTV는 겹쳐진 도형을 겹쳐지지 않은 상태가 되기 위한 최소한의 벡터를 말한다.
MTV를 구하기 위해서는 각 검사 축(Axis)에서 투영해서 나온 겹쳐진 길이의 최대값(스칼라)에 최대값이 나온
검사 축(벡터)을 곱셈한다. 이 값은 대상 도형이 이동해야 할 벡터를 의미한다.
MTV의 방향 결정
도형을 이동시키기 전에 한가지 알아내야 할 사항이 있다. "내가 구한 MTV가 도형의 바깥으로 가는 벡터인가, 도형 내부로
들어가는 벡터인가?"
한가지 예를 들자면 이동 가능한 도형 A가 왼쪽에 있고 고정된 도형 B가 오른쪽에 있다고 하자.
이 두 도형의 충돌을 검사하여 MTV를 구했고 도형 A는 MTV만큼 이동했다.
그러나 A 도형이 B도형 우측에 위치해있을 때 충돌후 MTV만큼 이동했을 때, A 도형은 B도형 내부로 파고들어가게 된다.
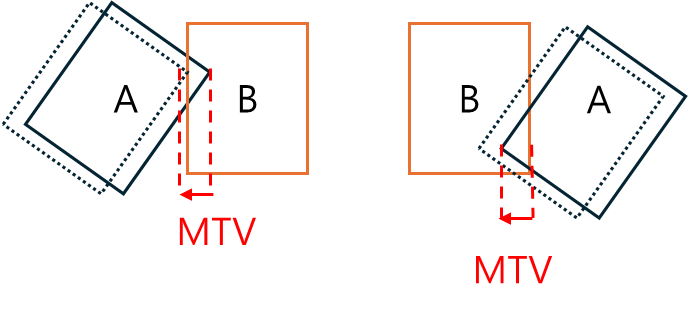
해당 현상이 발생하는 원인은 MTV를 산출해 낼 때 사용한 Axis 벡터는 오직 하나의 방향만 가르키기 때문이다.
그러므로 두 도형 위치 관계에 따른 MTV 방향을 설정 해주어야 한다.
우선 두 도형의 위치관계를 파악하기 위해 각 도형의 중점(Center Point)을 구한 후, 두 중점을 통해 하나의 벡터로
만든 후, MTV 벡터와 dot product 연산을 수행한다. 만약 dot 결과 값이 음수로 나온다면 두 벡터의 방향은 서로 반대
방향이 되므로 이 때 MTV의 방향도 반대로 연산시키면 된다.
참고한 사이트
- https://www.sevenson.com.au/programming/sat/
- https://www.youtube.com/watch?v=-EsWKT7Doww
- https://www.youtube.com/watch?v=dn0hUgsok9M&t=69s
- https://www.youtube.com/watch?v=gYZaiuz8pJU
'SFML' 카테고리의 다른 글
| SAT 이론 및 구현 스터디(2) (0) | 2025.03.05 |
|---|---|
| [SFML] 이벤트 다루어보기 (2) | 2025.01.10 |
| [SFML] SFML 창(window)을(를) 띄우고 관리까지 해보자. (0) | 2025.01.07 |
| [SFML] SFML 3.0 Visual Studio 개발 환경 구축하기 (2) | 2025.01.06 |
| SFML 알아보기 (2) | 2025.01.06 |
